Dep. of Instrumentation and Control Engineering
Ústav přístrojové a řídicí techniky
Dep. of Instrumentation and Control Engineering
Uncategorized

Design and analysis of spatially symmetric multi-dimensional delayed resonators

Published -Updated

Wim Michiels1, Senior Member, IEEE, Tomas Vyhlidal2, Karel Kraus3, Zbynek Sika3

1Department of Computer Science, KU Leuven, Leuven, 3001, Belgium,  
e-mail: wim.michiels@cs.kuleuven.be
2Department of Instrumentation and Control Engineering, Faculty of Mechanical Engineering, Czech Technical University in Prague, Technicka 4, 16000, Prague 6, Czechia,  
e-mail: tomas.vyhlidal@fs.cvut.cz
3Department of Mechanics, Biomechanics and Mechatronic, Faculty of Mechanical Engineering, Czech Technical University in Prague, Technicka 4, 16000, Prague 6, Czechia,  
e-mail: karel.kraus@fs.cvut.cz, zbynek.sika@fs.cvut.cz

Abstract

The contribution of the paper is three-fold. First, a novel, spatially symmetric two-dimensional vibration absorber is proposed. Structural conditions are given for unified frequencies and damping ratios, which lead to a one-parameter family of absorbers. Local proportional delayed feedback control laws are then derived that turn the absorber into an ideal absorber with assignable resonance frequency, which generalizes the delayed resonator. Second, it is proven that the time-averaged power requirement of the actuators in operation, deployed to compensate damping and adjust the resonance frequency to the one of a harmonic excitation force, as well as  the stability  of the controlled absorber, do not depend on the geometry of the unified absorber. However, the power distribution over the links strongly depend on the geometry, as illustrated with a comparison between the new symmetric configuration and a previously proposed asymmetric one. Third, the generalization to spatially symmetric three-dimensional absorbers is addressed. Among other results, it is shown that all admissible spatial configurations for  unified frequencies and damping ratios are identical up to reflection and rotation, in sharp contrast to the two-dimensional setting.

Draft paper link: http://hdl.handle.net/10467/120164
Final paper link: [to be inserted later]
Data link: [to be inserted later]

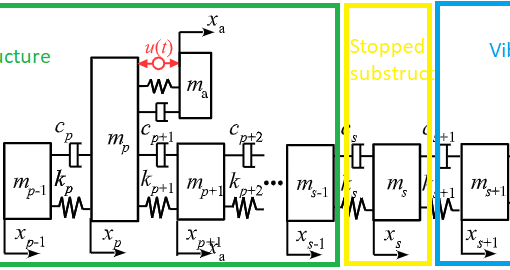
Results from the simulation case study 

Parameters of the symmetric 2D unified \((\zeta,\Omega)\)-absorber

mass: \(m=4.072\,\mathrm{kg}\)
moment of inertia: \(\mathcal{I}=0.1675\,\mathrm{kgm^2}\) 
diameter: \(R=0.2021\,\mathrm{m}\)
link stiffness: \(k=3264\,\mathrm{Nm^{-1}}\) 
link damping: \(c=5.404\,\mathrm{Nsm^{-1}}\) 
link length: \(D=0.25\,\mathrm{m}\) 
link angle: \(\theta=0.7819\) 

natural frequency: \(\Omega={34.675}\,\mathrm{s^{-1}}\)
damping: \(\zeta=0.0287\)

Parameters of the Stewart-like asymmetric 2D unified \((\zeta,\Omega)\)-absorber

Designed with the same mass, moment of inertia, natural frequency and the damping as for the symmetric absorber. 

mass: \(m=4.072\,\mathrm{kg}\)
moment of inertia: \(\mathcal{I}={0.1675}\,\mathrm{kgm^2}\)
length: \(L={0.5736}\,\mathrm{m}\)
center position: \(d={0.1434}\,\mathrm{m}\)
link stiffness: \(k_1={2448}\,\mathrm{Nm^{-1}}\), \(k_2={4896}\,\mathrm{Nm^{-1}}\), \(k_3={2448}\,\mathrm{Nm^{-1}}\)
link damping: \(c_1={4.053}\,\mathrm{Nsm^{-1}}\), \(c_2={8.106}\mathrm{Nsm^{-1}}\), \(c_3={4.053}\mathrm{Nsm^{-1}}\)

natural frequency: \(\Omega={34.675}\,\mathrm{s^{-1}}\)
damping: \(\zeta=0.0287\)

Parameters of the platform

Model adapted from the Appendix B of: Šika, Z., Vyhlídal, T., & Neusser, Z. (2021). Two-dimensional delayed resonator for entire vibration absorption. Journal of Sound and Vibration, 500, 116010. https://doi.org/10.1016/j.jsv.2021.116010  

mass: \(m_p={20}\,\mathrm{kg}\)
moment of inertia: \(\mathcal{I}_p={ 11.56}\,\mathrm{kgm^2}\)
link stiffness: \(k_x={10000}\,\mathrm{Nm^{-1}}\), \(k_y={10000}\,\mathrm{Nm^{-1}}\), \(k_\varphi={10000}\,\mathrm{Nm^{-1}}\)
link damping: \(c_x={116.72}\,\mathrm{Nsm^{-1}}\), \(c_y={98.76}\,\mathrm{Nsm^{-1}}\), \(c_\varphi={100}\,\mathrm{Nsm^{-1}}\)

Center of mass of the primary unified with the center of mass of the absorber, for both the considered cases. For the asymmetric, it yields \(\xi_A={-0.4302}\,\mathrm{m}\), and \(\eta_A={-0.1434}\,\mathrm{m}\).

Excitation force

magnitude: \(F={20}\,\mathrm{N}\)
frequency: \(\Omega={28.589}\,\mathrm{s^{-1}} ({4.55}\,\mathrm{Hz})\)

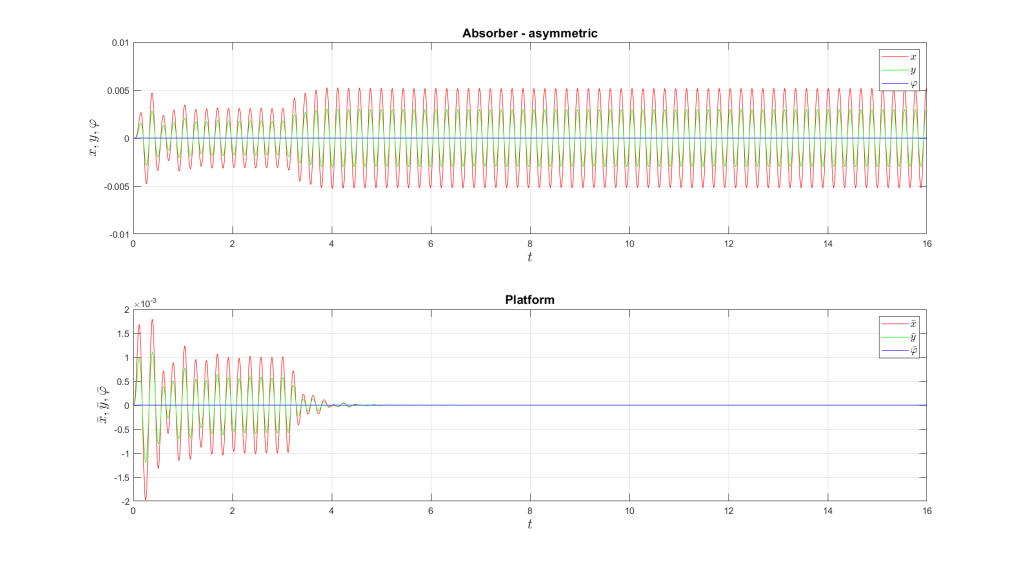
Case 1

Force position: \(x_F={0.3}\,\mathrm{m}\), \(y_F={0.4}\,\mathrm{m}\)
Force angle: \(\alpha={30}\,\mathrm{^{\circ}}\)
Force projection: \(F_x={17.320}\,\mathrm{N}\), \(F_y={10}\,\mathrm{N}\), \(T={-3.928}\,\mathrm{Nm}\)

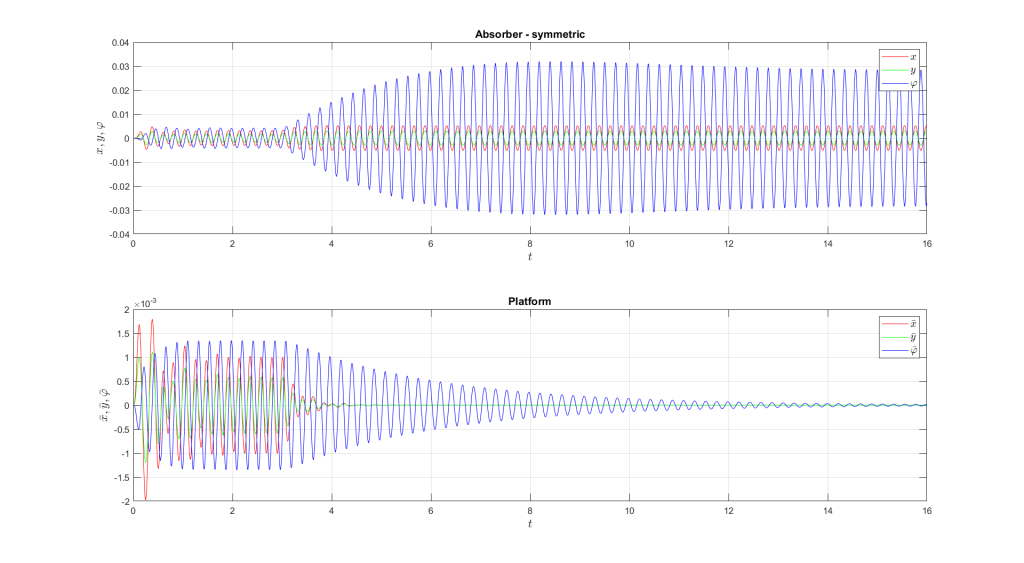
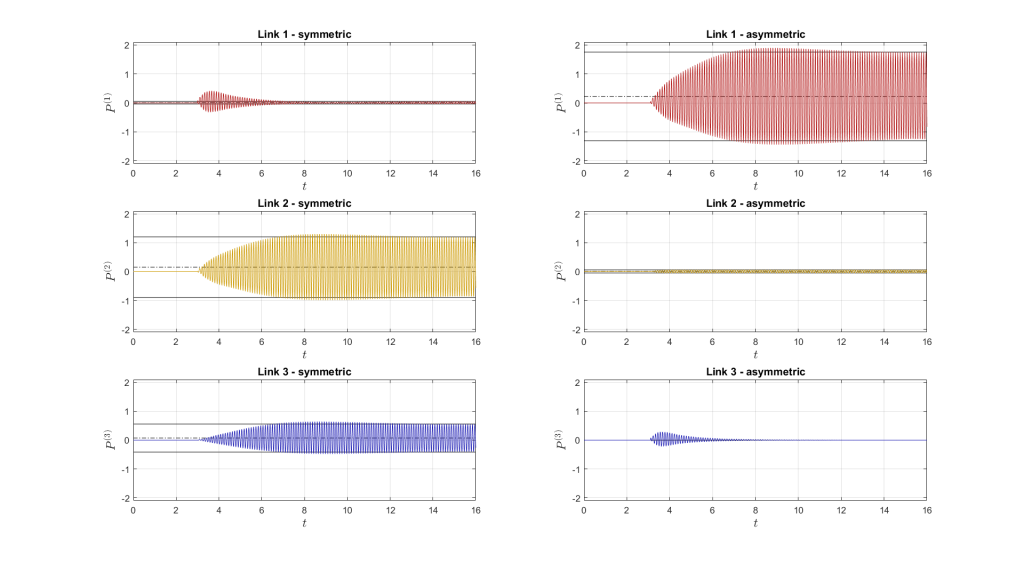
Case 1 – Simulation results – identical for both absorbers due to the structural decoupling and 2D unified \((\zeta,\Omega)\)-absorber features. The active feedback turned on at \(t={3}\,\mathrm{s}\). 

Power in the links

 Symmetric Asymmetric 
 Average P [W] Amplitude A [W] Average P [W] Amplitude A [W] 
Link 1 0.0063 0.0434 0.2238 1.5308 
Link 2 0.1540 1.0530 0.0080 0.0548 
Link 3 0.0715 0.4892 0 0 
Case 1 – Power supply in the links

Case 1 – Animation video – for visualization reasons, the motion and angular deflections are \(10\times\) amplified.

Case 2

Force position: \(x_F={0}\,\mathrm{m}\), \(y_F={0}\,\mathrm{m}\)
Force angle: \(\alpha={30}\,\mathrm{^{\circ}}\)
Force projection: \(F_x={17.320}\,\mathrm{N}\), \(F_y={10}\,\mathrm{N}\), \(T={0}\,\mathrm{Nm}\)

Case 2 – Simulation results – identical for both absorbers due to the structural decoupling and 2D unified \((\zeta,\Omega)\)-absorber features. The active feedback turned on at \(t={3}\,\mathrm{s}\).

Power in the links

 Symmetric Asymmetric 
 Average P [W] Amplitude A [W] Average P [W] Amplitude A [W] 
Link 1 0.0746 0.5099 0.0558 0.3817 
Link 2 0.0396 0.2708 0.0080 0.0548 
Link 3 0.0055 0.0375 0.0558 0.3817 
Case 2 – Power supply in the links

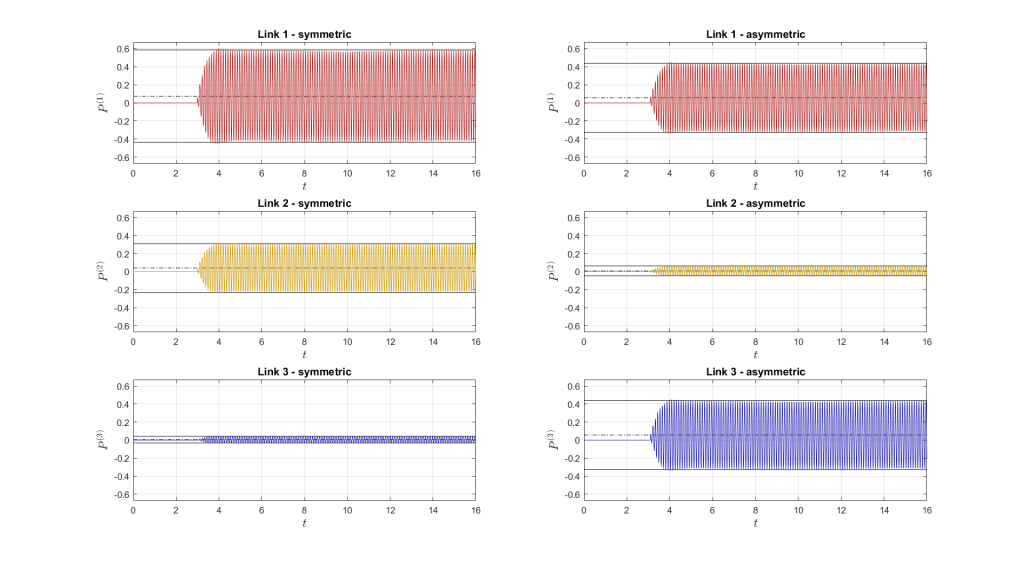
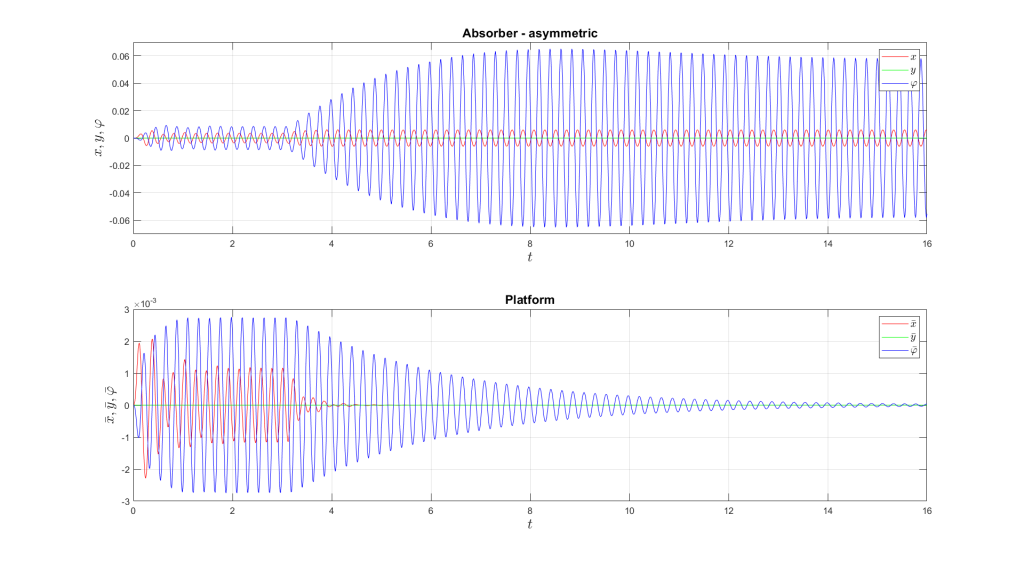
Case 2 – Animation video – for visualization reasons, the motion and angular deflections are \(10\times\) amplified.

Case 3

Force position: \(x_F={0.3}\,\mathrm{m}\), \(y_F={0.3}\,\mathrm{m}\)
Force angle: \(\alpha={30}\,\mathrm{^{\circ}}\)
Force projection: \(F_x={17.320}\,\mathrm{N}\), \(F_y={10}\,\mathrm{N}\), \(T={-3.928}\,\mathrm{Nm}\)

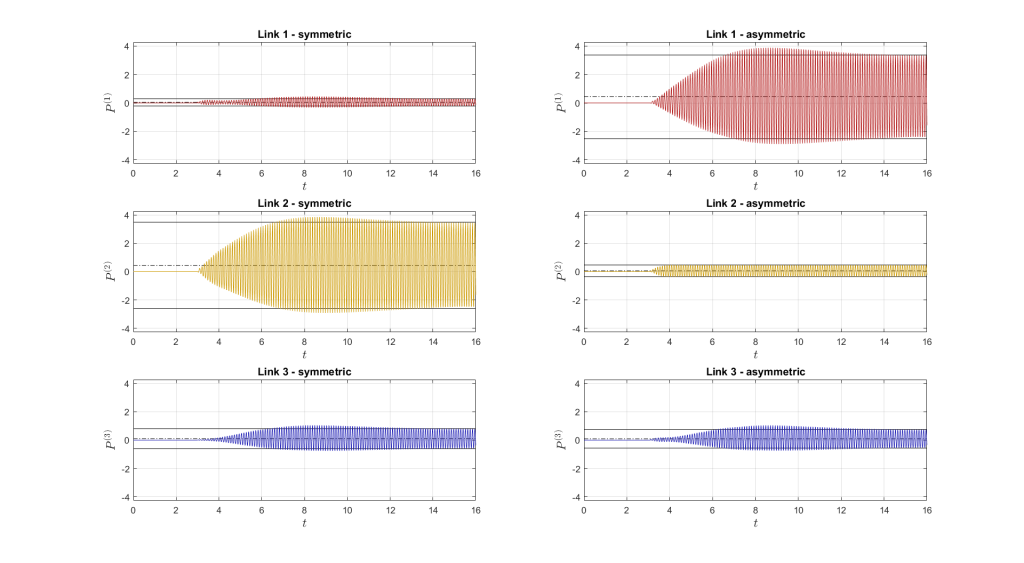
Case 3 – Simulation results – identical for both absorbers due to the structural decoupling and 2D unified \((\zeta,\Omega)\)-absorber features. The active feedback turned on at \(t={3}\,\mathrm{s}\). 

Power in the links

 Symmetric Asymmetric 
 Average P [W] Amplitude A [W] Average P [W] Amplitude A [W] 
Link 1 0.0374 0.2560 0.4294 2.9370 
Link 2 0.4441 3.0371 0.0598 0.4091 
Link 3 0.1035 0.7079  0.0957 0.6549 
Case 3 – Power supply in the links

Case 3 – Animation video – for visualization reasons, the motion and angular deflections are \(10\times\) amplified.

Case 4

Force position: \(x_F={0.3}\,\mathrm{m}\), \(y_F={0.4}\,\mathrm{m}\)

Case 4 – Simulation results – identical for both absorbers due to the structural decoupling and 2D unified \((\zeta,\Omega)\)-absorber features. The active feedback turned on at \(t={3}\,\mathrm{s}\). 

Power in the links

 Symmetric Asymmetric 
 Average P [W] Amplitude A [W] Average P [W] Amplitude A [W] 
Link 1 0.2838 1.9408 0.4651 3.1809 
Link 2 0.5798 3.9656 0.1196 0.8182 
Link 3 0.1028 0.7031 0.3817 2.6104 
Case 4 – Power supply in the links 

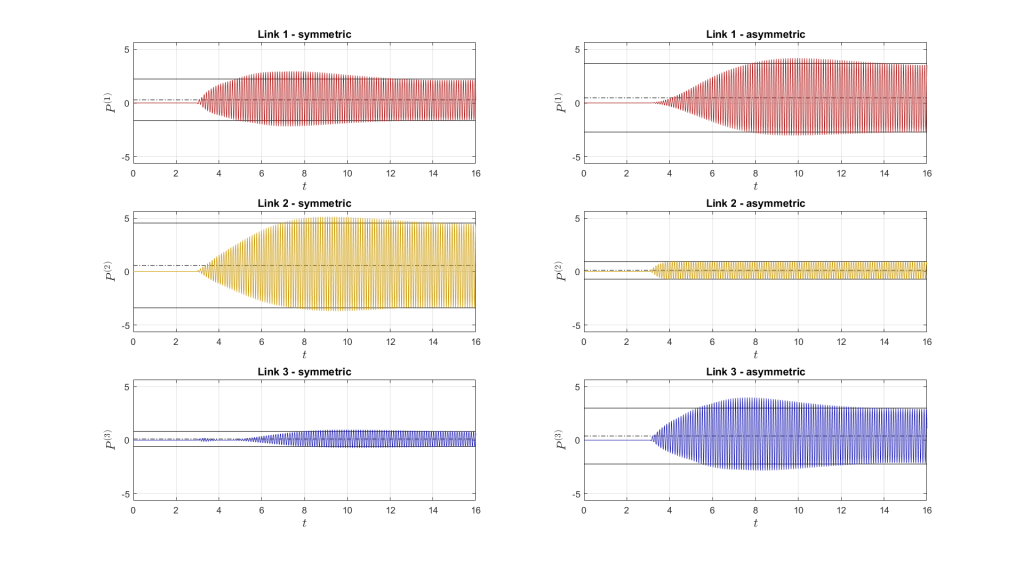
Case 4 – Animation video – for visualization reasons, the motion and angular deflections are \(10\times\) amplified. 

Case 5

Force position: \(x_F={0}\,\mathrm{m}\), \(y_F={0}\,\mathrm{m}\)

Case 5 – Simulation results – identical for both absorbers due to the structural decoupling and 2D unified \((\zeta,\Omega)\)-absorber features. The active feedback turned on at \(t={3}\,\mathrm{s}\). 

Power in the links

 Symmetric Asymmetric 
 Average P [W] Amplitude A [W] Average P [W] Amplitude A [W] 
Link 1 0.0798 0.5455 0.0598 0.4091 
Link 2 0.0798 0.5455 0.1196 0.8182 
Link 3 0.0798 0.5455 0.0598 0.4091 
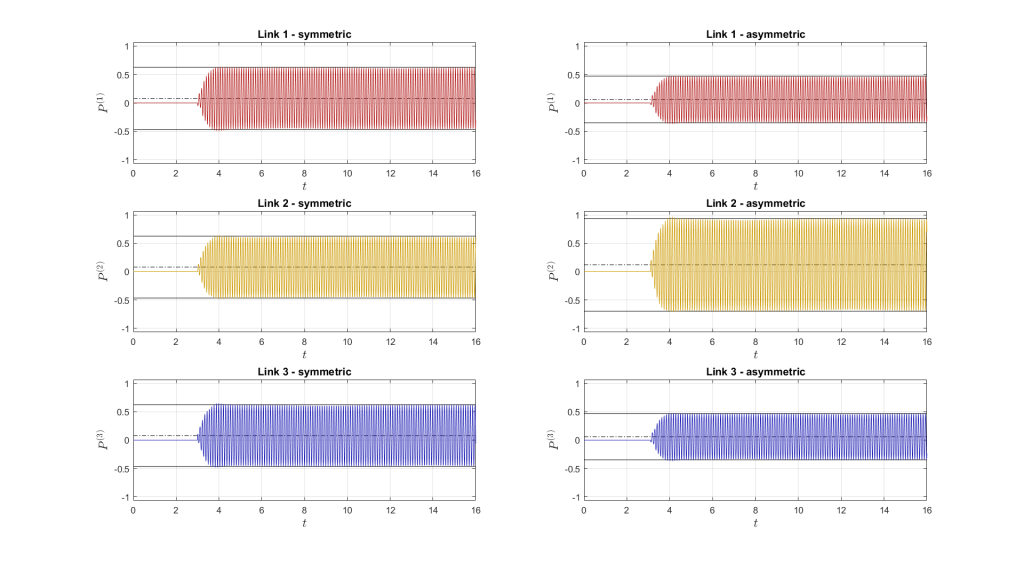
Case 5 – Power supply in the links 

Case 5 – Animation video – for visualization reasons, the motion and angular deflections are \(10\times\) amplified. 

Case 6

Force position: \(x_F={0}\,\mathrm{m}\), \(y_F={0}\,\mathrm{m}\)
Force angle: \(\alpha={135}\,\mathrm{^{\circ}}\)
Force projection: \(F_x={-14.1421}\,\mathrm{N}\), \(F_y={14.1421}\,\mathrm{N}\), \(T={0}\,\mathrm{Nm}\)

Case 6 – Simulation results – identical for both absorbers due to the structural decoupling and 2D unified \((\zeta,\Omega)\)-absorber features. The active feedback turned on at \(t={3}\,\mathrm{s}\). 

Power in the links

 Symmetric Asymmetric 
 Average P [W] Amplitude A [W] Average P [W] Amplitude A [W] 
Link 1 0 0 0 0 
Link 2 0.0601 0.4108 0.1196 0.8182 
Link 3 0.0596 0.4074 0 0 
Case 6 – Power supply in the links 

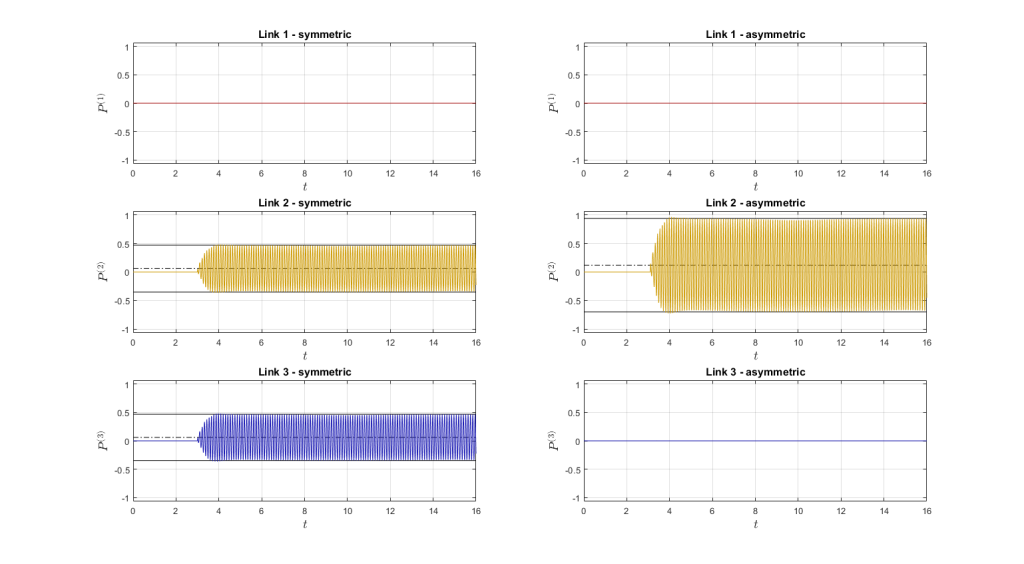
Case 6 – Animation video – for visualization reasons, the motion and angular deflections are \(10\times\) amplified. 

You may also like