A control design and numerical study is presented for the problem of maneuvering a quadcopter with suspended load. An inverse shaper with a distributed time delay is applied to the feedback path in order to pre-compensate the oscillatory mode of the two-body system. As the first step, the mode to be targeted by the inverse shaper is determined, which is neither the oscillatory mode of the overall system dynamics, nor the oscillatory mode of the suspended load. Next, the established cascade control scheme for UAVs with slave PD pitch angle controller and master PID velocity controller is adopted and supplemented by the inverse shaper tuned to the isolated flexible mode. The numerical and simulation based analysis reveals the key design aspects and dynamics features — due to including the inverse shaper with time delays, the closed loop system becomes infinite dimensional. As the main result, the positive effects of including the inverse shaper in the loop feedback are demonstrated. First of all, the oscillatory mode is well compensated when excited by both the set-point and disturbance changes. Besides, it is shown that the mode compensation is preserved even when reaching the saturation limits at the control actions.

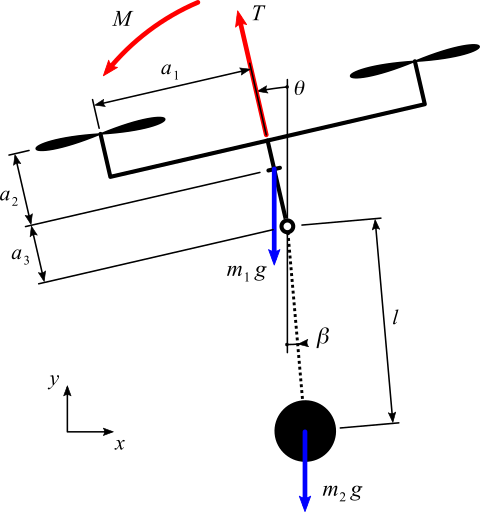
Fig. 2: Simulation based results of quadcopter with suspended load maneuvering with inverse shaper.
References
Bušek, J., Kuře, M., Hromčík, M., & Vyhlídal, T. “Control Design With Inverse Feedback Shaper for Quadcopter With Suspended Load.” Proceedings of the ASME 2018 Dynamic Systems and Control Conference. Volume 3: Modeling and Validation; Multi-Agent and Networked Systems; Path Planning and Motion Control; Tracking Control Systems; Unmanned Aerial Vehicles (UAVs) and Application; Unmanned Ground and Aerial Vehicles; Vibration in Mechanical Systems; Vibrations and Control of Systems; Vibrations: Modeling, Analysis, and Control. Atlanta, Georgia, USA. September 30–October 3, 2018. V003T40A009. ASME. https://doi.org/10.1115/DSCC2018-9052

